A comparative study on network alignment techniques
Summary
从矩阵对齐和网络表示学习的角度总结了state-of-the-art的7种方法,并建立了一个统一的基准平台。同时他们还研究了不同网络因素对于这些方法的影响。
这篇文章对于7种方法的介绍非常详细(数学真得好难),可以参考。
但是数据集对于该问题是主要的影响因素,但是公开数据集特别少。
Research Objective
比较现有网络对齐的方法
评估公共框架下的 Network Alignment 技术
本研究的主要目的是提供一个灵活而强大的工具,以支持比较和促进网络对齐技术的基准分析。
Problem Statement
文章中将目前的 Network Align 方法分为 spectral methods(基于邻接矩阵的操作) 和 network representation methods (节点用嵌入向量表示,能够捕捉到网络的结构信息)
虽然Network Alignment方法的研究已经很长时间了,但由于缺少公共数据集和共同的评价指标,还没有比较过这些方法的性能。
Network alignment methods
网络对齐技术利用结构一致性和属性一致性假设来构建它们的模型。
结构一致性:同质性原则,即邻近的节点倾向于在不同的网络中维持它们之间的关系
属性一致性:属于同一身份的在不同网络上的节点可能保持相同的属性(特征)
Spectral methods — matrix factorization 矩阵分解
使用矩阵分解,直接计算对齐矩阵 S
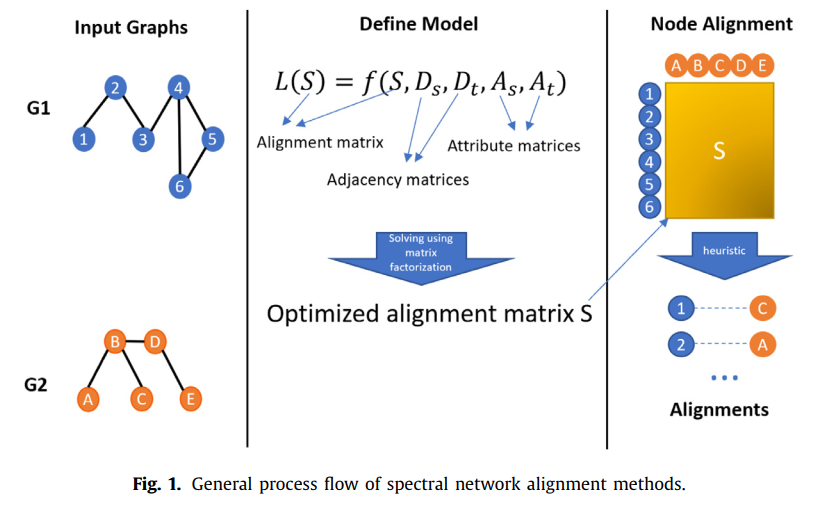
将输入的图用连接矩阵的形式表示,Spectral methods 以损失函数的形式定义模型,模型考虑了源和目标网络的邻接矩阵;节点特征为常量,对齐矩阵S为变量。在对准过程中,根据结构和/或属性一致性假设,通过优化损失函数来学习得到对准矩阵。
Spectral methods 不同之处在于构建模型时使用什么一致性原则以及该原则如何使用的
IsoRank:如果来自不同网络的两个节点的邻居是相似的,那么这两个节点是相似的。因此该方法中,节点的相似性取决于两个节点邻居的相似性。
similarity:
该方法对于网络的结构较敏感
BigAlign
利用网络节点的原始特征和手工提取的特征,如节点度、权重、集群系数等,将源网络和目标网络转换成二分图,从而解决网络对齐问题。
求置换矩阵 P,使损失函数最小化:
P 用于对 $D{s}$ 的行进行重新排序,$P^{t}$ 用于对 $D{t}$ 的列进行重新排序。难解。
将图转化成二分图然后最小化损失函数:
上面的损失函数可以通过 alternating projected gradient descent (APGD) 来优化:
仅用属性信息而忽略了拓扑信息。
FINAL
通过定义结构相似性、节点特征相似性和边特征的相似性条件
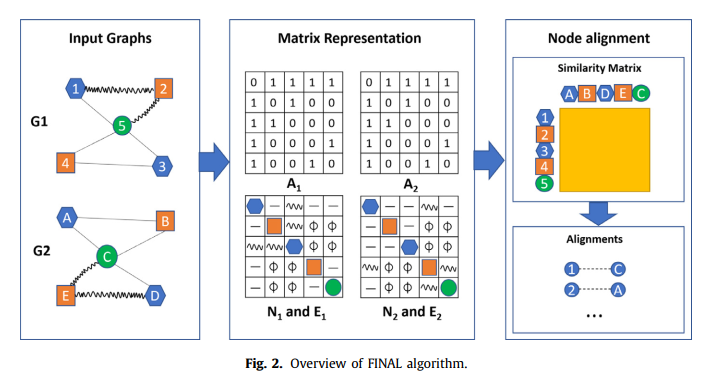
数学好难,没看懂。。。
REGAL
两个节点之间的相似性:
Representation learning methods
embedding generation 嵌入的生成
alignment matrix generation 对齐矩阵的生成
对于基于嵌入的网络对齐方法,不同之处在于embedding function 和 mapping function
PALE
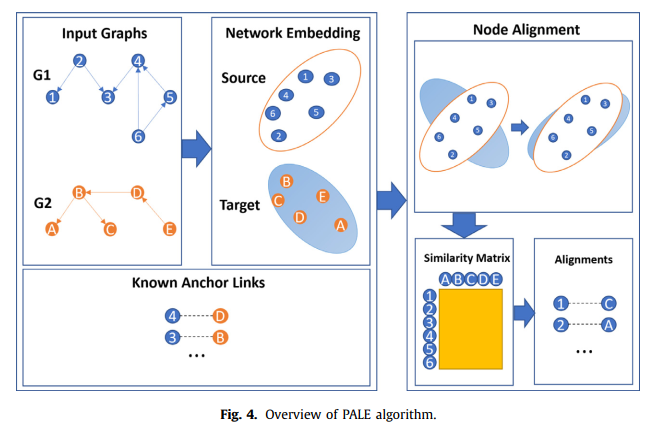
我之前的阅读笔记。
首先对网络进行扩展:如果在source网络中 $u_s$ 和 $v_s$存在边,并且知道这两个在target网络中对应的节点 $u_t$ 和 $v_t$, 那么 $u_t$ 和 $v_t$ 之间也应该有边,因此通过这样的方式扩展网络
Emdedding function
其中 $E$ 是 embedding matrix,它是通过最小化如下损失得到的:
其中 $(u,v) \in E$ 是观测到的边,$w$ 是通过在E中负采样的节点
Mapping function
$M$ 是一个$d×d$ 的矩阵,通过最小化下面的损失函数得到:
$H$ 是先验对齐矩阵
DeepLink
embedding graph 与PALE是一样的,但在mapping function中考虑了mapping的方向
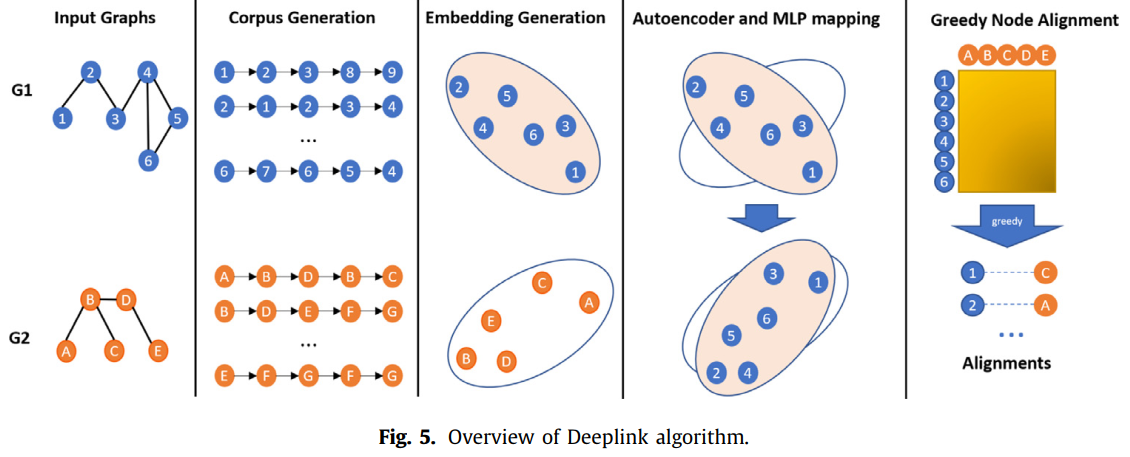
Emdedding function
参数 $E$ 的 loss function:
DeepLink方法认为如果 $v$ 是 $u$随机游走过程中的节点,则认为这两个节点相似。
Mapping function
从源网络 $G_s$ 到目标网络 $G_t$ 的 mapping function
类似的 从目标网络 $G_t$ 到源网络 $G_s$ 的 mapping function
参数 $\phi{s, t}$ 通过最优化如下loss function得到($\phi{t, s}$ 类似):
对于两个网络中的同一个用户,他们的嵌入向量应该是相似的,因此,通过最小化损失函数来改进 $\phi{s, t}$ 和 $\phi{t, s}$:
对于监督学习,最大化 reward function
https://tiantianliu2018.github.io/2019/09/15/%E8%AE%BA%E6%96%87%E9%98%85%E8%AF%BB%E3%80%8ADeepLink-A-Deep-Learning-Approach-for-User-Identity-Linkage%E3%80%8B/
之前的论文阅读笔记
又一大堆数学公式推导,好像没有看下去。IONE
IONE 与 PALE 的 mapping function 是相同的,但是其 embedding function 更加复杂,它在计算节点的嵌入时考虑了节点的邻居特征。
Embedding function
一个 embedding 矩阵,其中的每一行是由三个向量拼接到一起的:节点向量、输入上下文向量、输出上下文向量,最终其 embedding function 为:
该方法的思想是:一个节点的节点向量可以影响其邻居的输入上下文向量,而其邻居的节点向量可以影响其输出上下文向量。
为了学习 $E$, 该方法需要满足两个目标:
每个图中相邻的节点应该具有类似的节点嵌入
为了实现该目标,可以通过考虑一个节点向量相对于其邻居的输入上下文向量的贡献概率来实现:
其经验定义为:
类似的,一个节点向量对其邻居的输出上下文向量的贡献的概率及其经验定义:
$p_1$ 应该和 $p_2$ 是相似的,于是有如下目标函数:
具有近似嵌入的节点是很好的对齐节点的候选节点
在两个网络中,两个节点如果是同一个用户,那么这两个节点是可以相互代替的,其代替的程度应该是由这两个节点是同一个用户的可信度确定的,基于这一点,对目标函数L1进行修改,将相应节点的信息考虑如下:
最终通过最小化联合目标函数,得到嵌入的参数
Mapping function
IONE的映射函数是PALE的映射函数的一个特例,映射矩阵M是单位矩阵
[https://tiantianliu2018.github.io/2019/09/30/%E8%AE%BA%E6%96%87%E9%98%85%E8%AF%BB%E3%80%8AAligning-Users-Across-Social-Networks-Using-Network-Embedding%E3%80%8B/](https://tiantianliu2018.github.io/2019/09/30/论文阅读《Aligning-Users-Across-Social-Networks-Using-Network-Embedding》/) 之前的论文阅读笔记
Methods
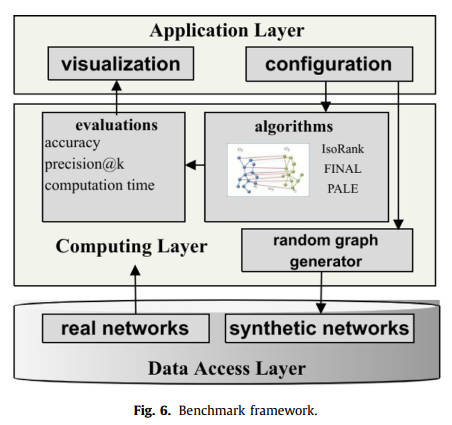
Datasets
Real-world datasets:这些数据集的质量好像都不太高
- S1. Douban online vs Douban offline
- S2. Flickr vs Lastfm
- S3. Flickr vs MySpace
- S4. Twitter vs Facebook
- S5. Twitter vs Foursquare
Synthetic datasets
- Partial synthetic:用真实网络生成目标网络
- Full synthetic:
Evaluation
Metrics
Accuracy
Precision@k
Mean Average Precision (MAP)
Evaluation procedure
- Structural noise level
- Attribute noise level
- Graph size
- Graph size imbalance
- Graph density
- Graph connectivity
- Number of connected components
Experimental evaluation
评估以上因素对于实验的影响
Conclusion
克服真实网络中的结构和属性不稳定性是网络对齐面临的主要挑战之一
Notes
- 本文作者: Kelly Liu
- 本文链接: http://tiantianliu2018.github.io/2019/10/07/论文阅读《A-comparative-study-on-network-alignment-techniques》/
- 版权声明: 本博客所有文章除特别声明外,均采用 MIT 许可协议。转载请注明出处!
